| The
tesseract: visualising a whole new world!
Martin
Drinkwater
Many people
consider 'dimensions' as a physical thing that they can
observe: a line, an irregular shape or a cube, for instance.
Having two eyes allows us to view an object from two different
angles, known as stereovision. This means that we can
learn to perceive depth from visual cues in three dimensions.
If you cover one eye and look at the world through only
one eye, you will only perceive a flat, two-dimensional
world.
Most of us
are hard-pressed to imagine something that is 4 or even
5 dimensions because this is outside the area of our experience.
Mathematicians, however, think of dimensions as something
entirely different – an infinite number of dimensions
can exist. These dimensions are quite rigorously defined,
which has resulted in the assignment of fractal (fractional)
dimensions as well as whole number ones. All this 'dimensionalising'
can lead to theoretical structures with amazing and unusual
properties.
For
instance, think of a point. Project a point in one direction
and you have a line. Project a segment of this line into
another dimension perpendicular to the line – giving a
total of 2 dimensions – and you create a square or rectangle.
Projecting a square into another dimension results in
a cube. Using this analogy, we can construct figures with
any number of dimensions, although visualising them can
lead to severe headaches!
The most commonly
studied higher-dimensional structure is the extension
of cube into another dimension, called a tesseract. There
is no mystery as to why the extension of the cube into
further dimensions is studied so much - this '4D' entity
is the simplest to visualise. Visualising is by no means
an easy task: the tesseract consists of 8 cubes, each
restricted to the same line segment on a single plane
and 3 squares meeting at each edge. The structure has
a total of 24 faces, 16 vertices and 32 edges. You can
create a shadowing effect by visualising each cube in
3D space, and use your perceptual vision to see the position
of the others relative to it.
Confused?
To aid in the process, go to Alexander
Bogomolny's website and view the Java applet-based
graphical explanation. These images highlighting one of
the cubes (in three different orientations) come from
that website.
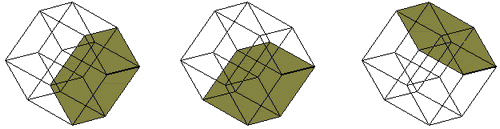
Potentially,
this process can be extended to an infinite number of
dimensions. The limiting factor is our ability to perceive
these figures or shapes and what we consider to be a ‘dimension’.
For instance, in physics, there are quantitative variables
to which we have assigned 'dimensions': metres, seconds,
coulombs just to name a few. Problems arise in that many
of these are defined in terms of other quantities - it
can be argued that the Earth's gravitational constant
for example (6.67x10-11
m3/s2.kg) has 6 dimensions.
These quantities are dimensional in a different sense
- they give us different ways of looking at the geometric
properties of free space.
To
complicate things further, there are also 'dimensionless'
quantities related to angles such as the radian (the angle
that one plane makes with another plane) and steradian
(the angle that one solid makes against another). Scientists
view these angles as being dimensionless because they
do not have an effect on the construction of the object.
Our
problem lies with what the term ‘dimension’ is supposed
to represent. There is the use of dimensions to define
variables and reduce uncertainty, which is in contrast
to our geometric interpretation of space. They are mutually
exclusive – one cannot be applied to the other. So we
can have infinitely many dimensions in a theoretical context
(when assigning variables), but we can only perceive
figures in these dimensions within certain geometrical
limits... Give me the good old squares and cubes anyday!
For
more information see Alexander Bogomolny's "Generalizations
in Mathematics" at cut-the-knot.org
See OnSET's The
Magic Eye
|